树作为一种逻辑结构，同时也是一种分层结构，具有以下两个特点： 1）树的根结点没有前驱结点，除根结点外的所有结点有且只有一个前驱结点。 2）树中所有结点可以有零个或多个后继结点。

树

树的概念

由 n（n>=0）个节点组成，有层次关系的集合。用图形表示像一颗倒挂的树。n=0时为空树

树适合表示具有层次结构的数据，树种的某个结点最多只和上一层的一个结点（即其父结点）有直接关系，因此在n个结点的树中有n-1条边。

一些名词解释

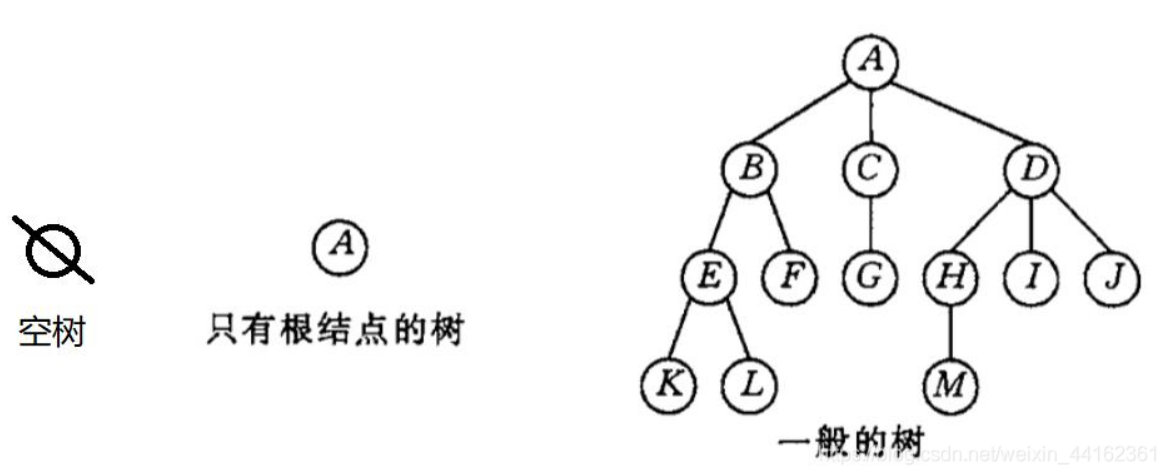
• 节点的度：一个节点含有的子树的个数，叫做该节点的度。
• 叶节点和终端节点：度为零的节点。
• 双亲结点或父节点：如图，C为G的父节点。
• 孩子节点或子节点：如图，G为C的子节点。
• 兄弟节点：拥有相同父节点的节点称为兄弟节点。
• 树的度：一棵树中最大的节点的度称为树的度。
• 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推。
• 树的高度或深度：树中节点的最大层次，如图，高度为4。
• 祖先：从跟到该节点所经分支上的所有节点。A是所有节点的祖先。
• 森林：由 m（m>0）棵互不相交的树的集合称为森林。

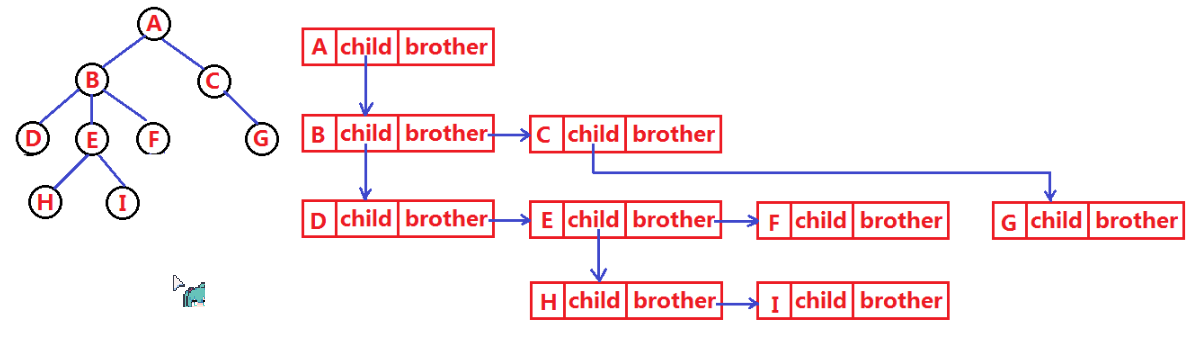
树的表示

C
typedef int DataType;
struct Node{
    struct Node* _First_Child_Ptr;   //  第一个子节点指针
    struct Node* _Bro_Ptr;          // 兄弟节点
    DataType _data;
};

二叉树

特点

1. 每个节点最多有两个子节点，即节点的度不超过2
2. 二叉树有左右之分，左右两个节点的顺序不能颠倒

性质

1. 若规定根节点为第 1 层，则一颗非空二叉树的第 i 层上最多有 2^(i-1) 个结点。

2. 若规定根节点为第 1 层，则深度为 h 的二叉树的最大总结点数为 2^h-1。

3. 任何一个二叉树，如果度为0，其叶结点个数为n0，度为2的分支结点个数为n2，则有n0 = n2 + 1。

4. 若规定根节点为第 1 层，具有 n 个结点的满二叉树的深度 h=log2(n+1)。

5. 对于具有 n 个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从 0 开始编号，则对于序号为 i 的结点有： （1）若 i > 0，i 位置节点的双亲序号：(i-1)/2；i = 0，i 为根节点编号，无双亲节点。

   （2）若 2i+1 < n，左孩子序号：2i+1；2i+1 >= n否则无左孩子。

   （3）若 2i+2 < n，右孩子序号：2i+2；2i+2 >= n否则无右孩子。

特殊的二叉树

满二叉树

每层的结点都达到最大值，则这个二叉树就是满二叉树。反过来说，如果一个二叉树的从层数为 K 且结点总数为 2^k - 1，则为满二叉树。

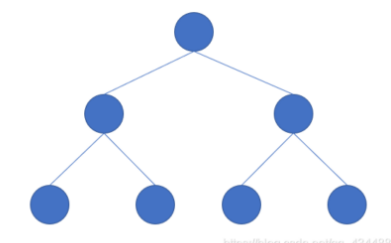
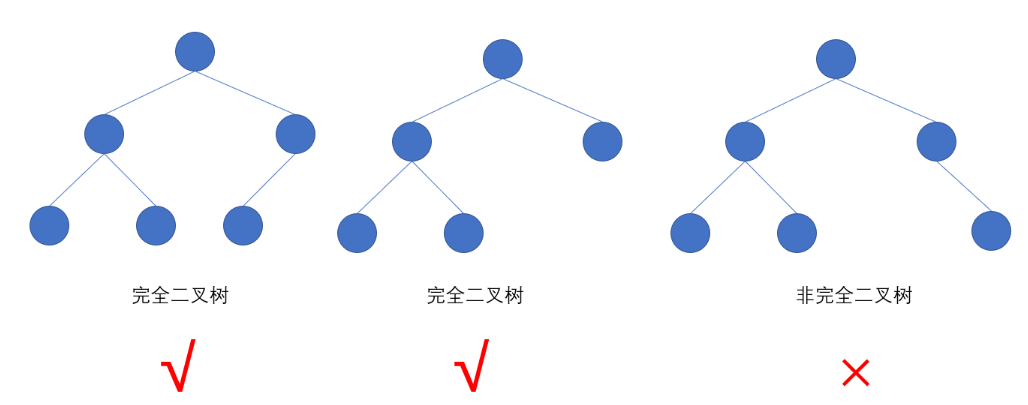
完全二叉树

满二叉树要求每一层的结点树都达到最大值，完全二叉树仅要求除最后一层外的节点树达到最大值，最后一层可以不满，并且最下⾯⼀层的节点都集中在该层最左边的若⼲位置。可以把满二叉树看成一种特殊的完全二叉树。

二叉搜索树

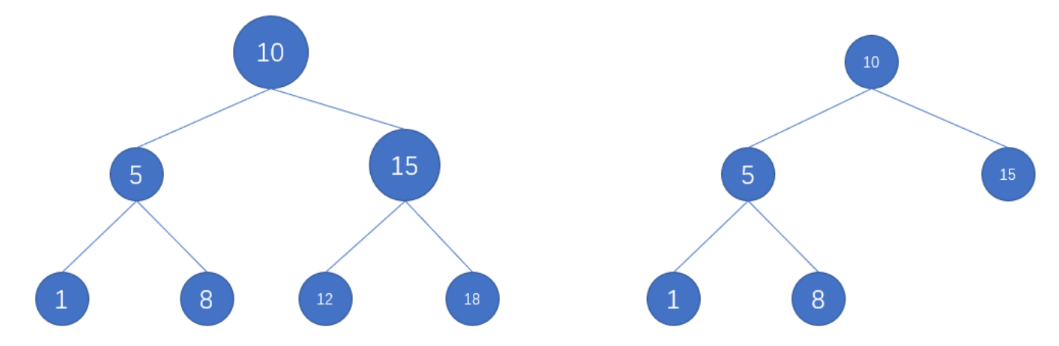
 ⼆叉搜索树是有数值的，⼆叉搜索树是⼀个有序树。

• 若它的左⼦树不空，则左⼦树上所有结点的值均⼩于它的根结点的值；
• 若它的右⼦树不空，则右⼦树上所有结点的值均⼤于它的根结点的值；
• 它的左、右⼦树也分别为⼆叉搜索树。

平衡二叉搜索树（AVL树）

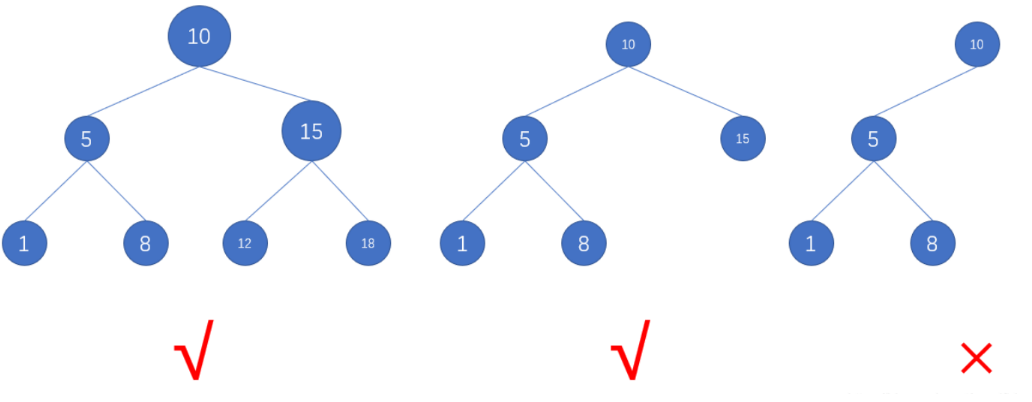
平衡⼆叉搜索树⼜被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：

1. 它是⼀棵空树或它的左右两个⼦树的⾼度差的绝对值不超过1，并且

2. 左右两个⼦树都是⼀棵平衡⼆叉树。